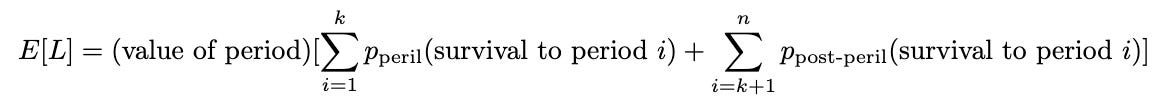Sensitive assumptions in longtermist modeling
Crucial considerations in valuing the future

(Crossposted to the Effective Altruism Forum: post)
{Epistemic Status: Repeating critiques from David Thorstad’s excellent papers (link, link) and blog, with some additions of my own. The list is not intended to be representative and/or comprehensive for either critiques or rebuttals. Unattributed graphs are my own and more likely to contain errors.}
I am someone generally sympathetic to philosophical longtermism and total utilitarianism, but like many effective altruists, I have often been skeptical about the relative value of actual longtermism-inspired interventions. Unfortunately, though, for a long time I was unable to express any specific, legible critiques of longtermism other than a semi-incredulous stare. Luckily, this condition has changed in the last several months since I started reading David Thorstad’s excellent blog (and papers) critiquing longtermism.1 His points cover a wide range of issues, but in today’s post I would like to focus on a couple of crucial and plausibly incorrect modeling assumptions Thorstad notes in analyses of existential risk reduction, explain a few more critiques of my own, and cover some relevant counterarguments.
Model assumptions noted by Thorstad
1. Baseline risk (blog post)
When estimating the value of reducing existential risk, one essential – but non-obvious – component is the ‘baseline risk’, i.e., the total existential risk, including risks from sources not being intervened on.2
To understand this, let’s start with an equation for the expected life-years E[L] in the future, parameterized by a period existential risk (r), and fill it with respectable values:3
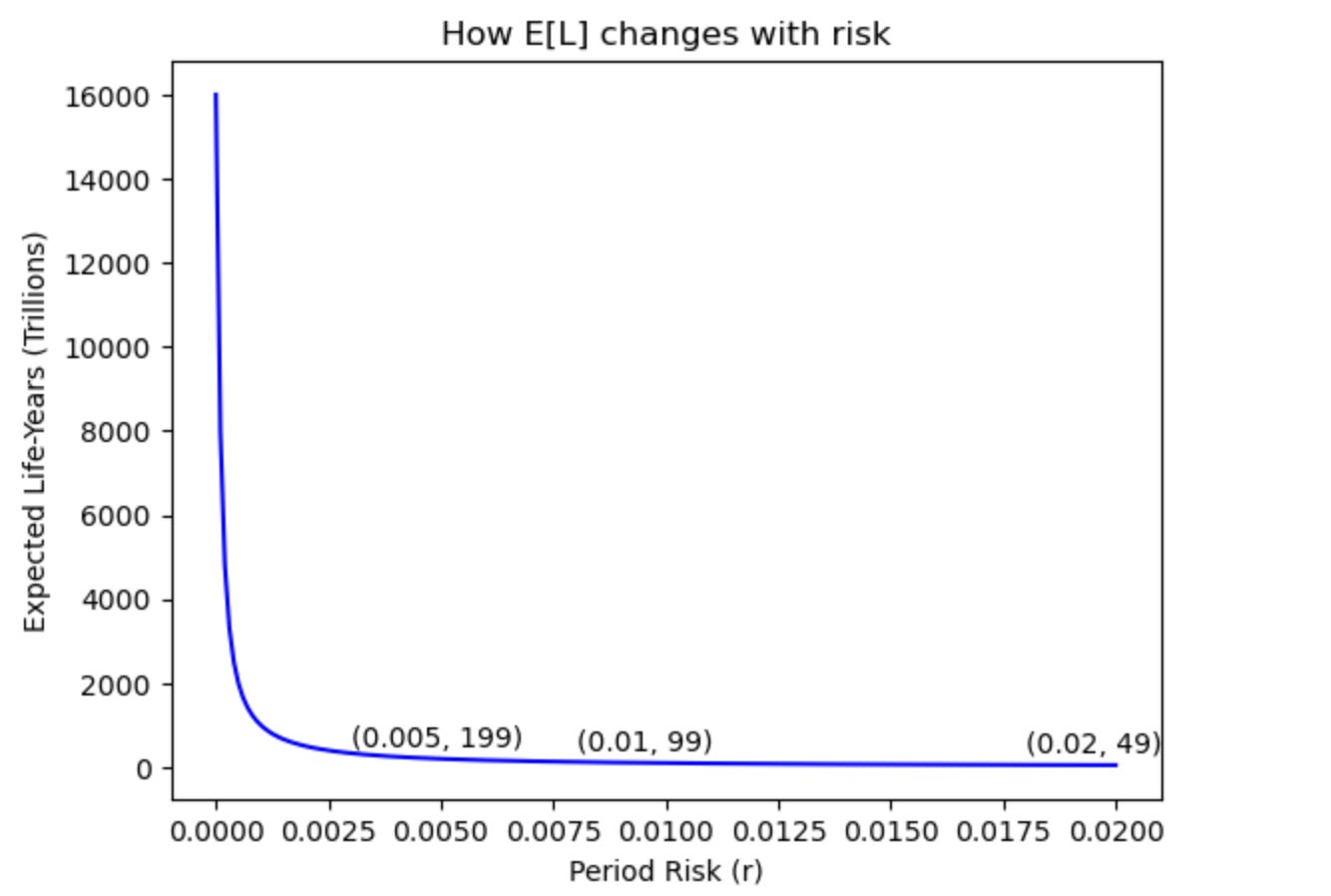
Now, to understand the importance of baseline risk, let’s start by examining an estimated E[L] under different levels of risk (without considering interventions):
Here we can observe that the expected life-years in the future drops off substantially as the period existential risk (r) increases and that the decline (slope) is greater for smaller period risks than for larger ones. This finding might not seem especially significant, but if we use this same analysis to estimate the value of reducing period existential risk, we find that the value drops off in exactly the same way as baseline risk increases.

Indeed, if we examine the graph above, we can see that differences in baseline risk (0.2% vs. 1.2%) can potentially dominate tenfold (1% vs. 0.1%) differences in absolute period existential risk (r) reduction.
Takeaways from this:
(1) There’s less point in saving the world if it’s just going to end anyway. Which is to say that pessimism about existential risk (i.e. higher risk) decreases the value of existential risk reduction because the saved future is riskier and therefore less valuable.
(2) Individual existential risks cannot be evaluated in isolation. The value of existential risk reduction in one area (e.g., engineered pathogens) is substantially impacted by all other estimated sources of risk (e.g. asteroids, nuclear war, etc.). It is also potentially affected by any unknown risks, which seems especially concerning.
2. Future Population (blog post)
When calculating the benefits of reduced existential risk, another key parameter choice is the estimate of future population size. In our model above, we used a superficially conservative estimate of 10 billion for the total future population every century. This might seem like a reasonable baseline given that the current global population is approximately 8 billion, but once we account for current and projected declines in global fertility, this assumption shifts from appearing conservative to appearing optimistic.
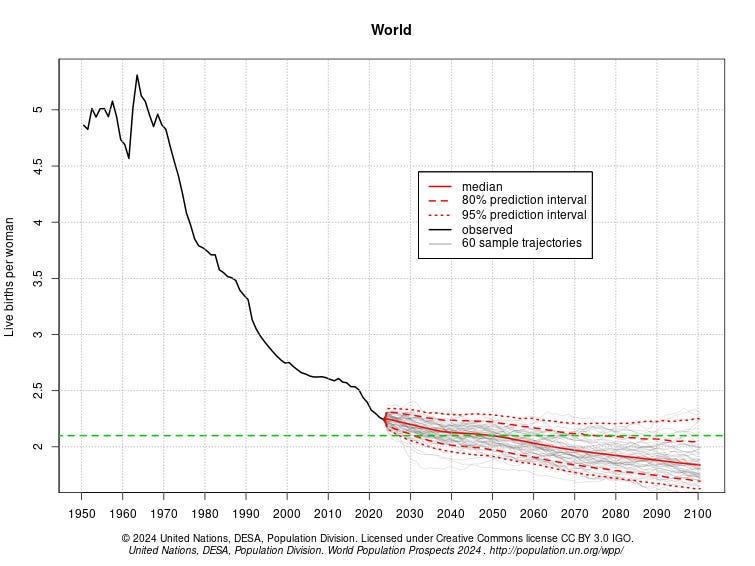
United Nations modeling currently projects that global fertility will fall below replacement rate around 2050 and continue declining from there. The effect is that total population is expected to begin dropping around 2100.
If you take the U.N. models and try to extrapolate them out further, the situation begins to look substantially more dire since fertility declines below replacement compound each generation to quickly shrink populations.

Takeaways from this:
(1) Current trends suggest that future populations may be substantially smaller than the current population. Neither growing nor constant future populations are presumable as default outcomes.
(2) The fewer people there are in the future, the less valuable it is to save. This effect can plausibly drop the value of existential risk reduction by nearly an order of magnitude (from 10 billion or more lives per century to 2 billion or fewer lives) on conservative estimates.4 Decreases can reach multiple orders of magnitude if original estimates are larger, such as from assuming population reaches carrying capacity.
Other model assumptions/considerations I think are important
1. Intervention decay
One important assumption made in the model above is that an intervention reduces period existential risk uniformly across centuries. This is an extremely implausible assumption. In order to understand the impact of this assumption, let’s model the decay of intervention effects with a constant discount factor each period.
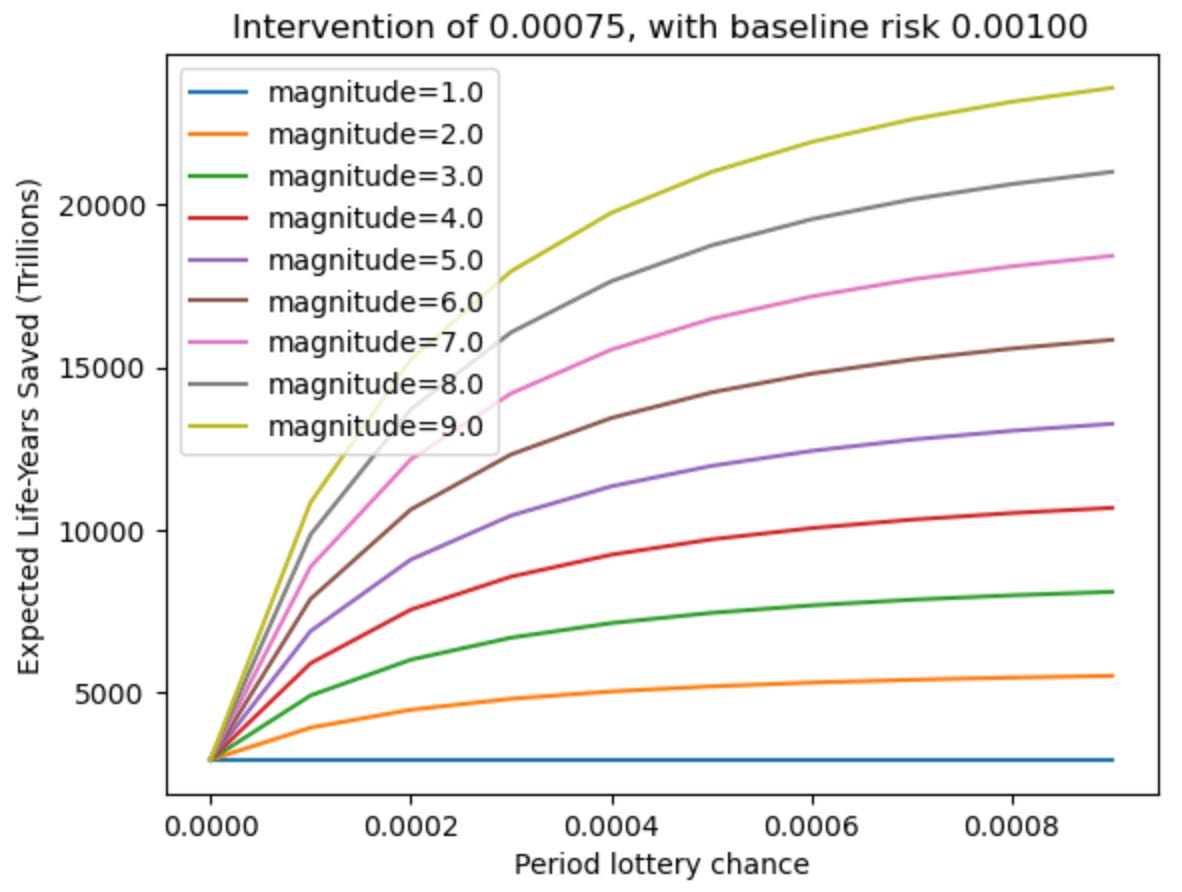
We can then see the effect of changing this new parameter on the value of existential risk reduction on our original model.

Looking at these estimate graphs, it seems clear that intervention decay has a substantial negative effect on the value of existential risk reduction, even in very optimistic scenarios. Moving from no discount to a discount of 0.99 per century can result in an estimated value decrease in the range of 80-97% (as seen above).
Takeaways from this:
(1) Introducing even very small intervention decay into our model can result in extremely diminished value of existential risk reduction.
(2) Intervention decay is likely to be much more severe for at least two reasons. First, continual effects require extremely strong inter-generational coordination or lock-in. Second, the risks faced by future civilizations are likely to be compositionally different from current risks. As a result, we should expect interventions today to have progressively less impact since new dangers will grow as a proportion of risk.
2. Suffering risks (S-risks)
In the original model, the value of an existing future is always positive, but this is obviously not guaranteed. Although mostly speculative, it is important to also take account of S-risks such as mass expansion of factory farming or unending and catastrophic war. To see the impact of these risks on our model, we can add two parameters, the probability of an S-risk and its severity, and see how they affect the value of existential risk mitigation. Here is the revised model:5
Now we can take a look at the model outputs.
First we have the super scary graph:

Looking at this graph you can observe the obvious point that if either the severity or period probability of an S-risk increases, then (all else held equal) the value of existential risk reduction decreases. Of course, while this graph gives a good view of the general distribution shape, my expectation is that both the probabilities and severities depicted are misleadingly large. For more conservative outputs, we can zoom in to the top left corner of the graph:

Takeaways from this:
(1) Unlike the previous items mentioned in this post, the question of whether S-risks have a strong effect on the benefits of existential risk reduction is debatable. It seems plausible to me that reasonable people would mostly agree that per-century risk is in the ‘one in a million or less’ bucket, but your priorage may vary. Regarding the severity of S-risks, I am considerably more uncertain, but I think the outcomes modeled above suggest that higher probabilities are more concerning than greater severity at the current margin.
(2) As before, the effect of interventions is strongly affected by baseline risk and the impact of S-risks can be highly variable across (intervention, baseline risk) pairs once for larger period S-risk probabilities. The variance is substantially smaller at low probabilities.
Counter-arguments for the value of existential risk reduction
1. The ‘time of perils hypothesis’ versus ‘baseline risk’ and ‘intervention decay’
The baseline risk assumption highlighted above seems to suggest that high existential risk estimates should decrease the expected value of existential risk reduction. Despite this, longtermist analysis often suggests there is both a high existential risk and a high value to longtermist interventions. This seems paradoxical until you account for the ‘time of perils hypothesis,’ which suggests that existential risk may be high and/or increasing right now, but that as civilization improves, risk will fall to extremely low levels following a Kuznets curve.
This new model can successfully save the value of longtermist interventions from both the baseline risk problem and intervention decay problem. The baseline risk problem is addressed by lowering future ‘after perils’ risk and the intervention decay problem is addressed by moving risk into periods where interventions have yet to decay. However, this new model requires both that the time of perils is short and that the reduction in risk is very substantial after the time of perils. We can adapt our original model by adding a new “time of perils” to our model:
Then we can see how the value of interventions changes with respect to new parameters.
Looking at these outputs, we can see that even after applying the time of perils hypothesis, estimates of the value of existential risk reduction are still substantially affected by baseline estimates for period existential risk (after the time of perils). As Thorstad has noted, these extremely low estimates for period risk seem especially implausible under the ‘time of perils’ hypothesis because the relative risk reduction needed to achieve low post-peril risk is substantially higher than if there were no ‘time of perils.’
Takeaways from this:
(1) The time of perils hypothesis can successfully defend the dual claim that existential risks are high and that reducing them is extremely valuable. However, endorsing this view likely requires fairly speculative claims about how existing risks will nearly disappear after the time of perils has ended.
(2) Even with the time of perils hypothesis, the value of existential risk mitigation is still highly impacted by small changes in estimated future risk.
2. Hedonic lotteries
Since I’ve discussed S-risks as a potentially important consideration, I feel it would be disingenuous to skip their positive mirror ‘hedonic lotteries’ which are potential symmetrically massive improvements in wellbeing. To model the effect of these in isolation, I will just use the S-risk model again, but with positive magnitudes, rather than negative ones. Here are the two ‘hedonic lottery’ versions of the graphs from the S-risk section.

Takeaways from this:
(1) Hedonic lotteries appear to be approximately (though not exactly) symmetric with S-risks in their effect on future value. Still, imbalances in either probabilities or magnitudes between the two can easily allow them to be impactful.
(2) Though not obvious from the two graphs above, baseline risk remains relevant for determining the impact of hedonic lotteries on the value of existential risk reduction.
Final thoughts
The main two factors motivating this post were (1) reading David Thorstad’s criticisms of longtermist analysis and (2) seeing that many of his critiques were presented only with point estimates, rather than more continuous graphs. I hope that this post managed to add some value on that second front.
I also want to note that the specific analysis in this post was fairly limited in terms of the models and values considered. That said, the considerations examined are likely relevant to many analyses. Ultimately, I think this is an area where a team like Rethink Priorities could improve general practice by creating an X-risk intervention value calculator.6 I have considered making such a tool myself, but haven’t gotten around to it.
That’s it! I will probably be returning to a much shorter format next time, so don’t worry if this one was too long for you. In the meantime, let me know if you think there were more sensitive variables or critiques I should have covered.
{Code used to generate plots is available at https://github.com/ohmurphy/longtermism-sensitivity-analysis/tree/main}
This was lucky insofar as it gave me a better way to explicitly model my doubts. In utility terms, I expect that this news is unfavorable since it mostly involves decreasing the expected value of the future.
Thorstad actually uses the ‘Background Risk’, which (I think) only contains risks outside the current intervention field. I’ve used ‘baseline risk’ to combine both domain and background risk since it seems simpler to me.
The constants here are set to approximately match the arrangement presented in Existential Risk and Cost-Effective Biosecurity, where the future is modeled with a “global population of 10 billion for the next 1.6 million years.” Periods are set as centuries, which is a difference from their model since they only use cumulative, rather than period risk. This was another point of criticism by Thorstad, but I decided to skip discussing it in this post. The equation used is approximately copied from Three Mistakes in Moral Mathematics of Existential Risk, but with the number of periods increased to better match the MSB paper.
It is also plausible that smaller populations would experience greater existential risk since smaller, catastrophic risks might become existential. This would further reduce the value of existential risk reduction.
This model assumes the S-risks are attractor states, so once reached they never return to a “normal” state. I think it would be worth modeling possible reversions explicitly, but I simplifying for the moment. I understand the irony.
Some ideas for inclusion: (1) parameter and equation options, (2) simple diagram generation, (3) highlighting of key assumptions (ones with high value of information), (4) estimates taken from different experts/research/forecasts made available as parameters, (5) ability to apply differing moral systems, (6) cost-effectiveness estimates relative to GiveWell recommendations.