Why would height be normally distributed?
Normality can be peculiar
{Epistemic Status: Just working through some confusion. The perspective taken here is purely mathematical, I am not an expert on biology, population statistics, or anything else in that vicinity. Conclusions here are for my satisfaction, results are not meant to be accurate to reality.}
One example of the normal distribution that is often used is the distribution of height in the population. At first brush, this seems like a straightforward idea, but, on closer inspection, I notice I am confused.
The Central Limit Theorem
Part of the reason that the normal distribution of height seems superficially unremarkable is that the normal distribution appears everywhere in real-world data and statistical models. The reason for this prevalence is demonstrated by the Central Limit Theorem (CLT),1 which states that the distribution of the sum (or average) of independent and identically distributed variables converges to the normal (Gaussian) distribution.
Looking at that definition, we can see three necessary and sufficient conditions for the CLT to apply:
(A1) The distribution is for a sum or average of variables X1, X2, etc.
(A2) X1, X2, etc. are independent.
(A3) X1, X2, etc. are identically distributed.
Application of CLT to height
Now that we have clear conditions for the CLT to apply, let’s compare them against what we know about height.
Here are three claims often made about height:
(B1) Human height is normally distributed.2
(B2) Differences in human height are strongly attributable (>60) to genetic factors.
(B3) Human height is strongly (>70%) heritable.
The fact that height empirically seems to follow a normal distribution is very suggestive that the CLT applies. Indeed, if you ask Chatgpt it will answer that the Central Limit Theorem is applicable to the distribution of height.
However, if we return to your necessary and sufficient conditions for the CLT to apply, it is not clear that they are satisfied. In particular, the assumption that variables are identically distributed seems clearly false in light of the heritable genetic influence on height. For the sake of clarifying, let’s go through some examples of how we could construct a normal distribution for height.
Example 1: Simple random sampling
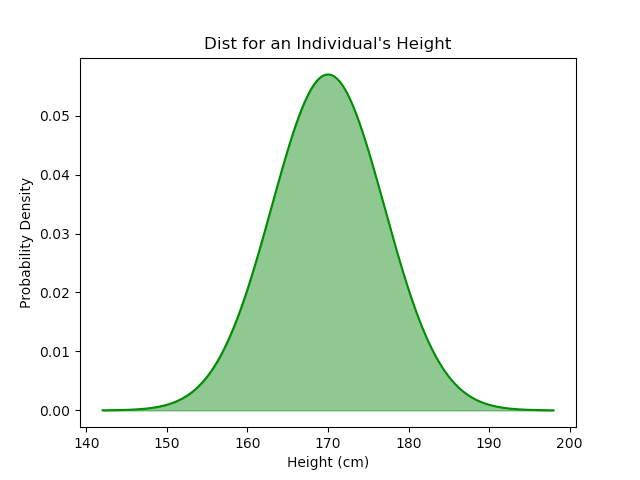
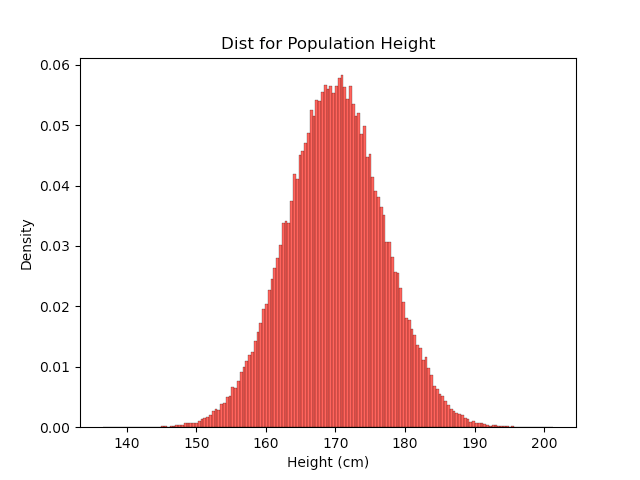
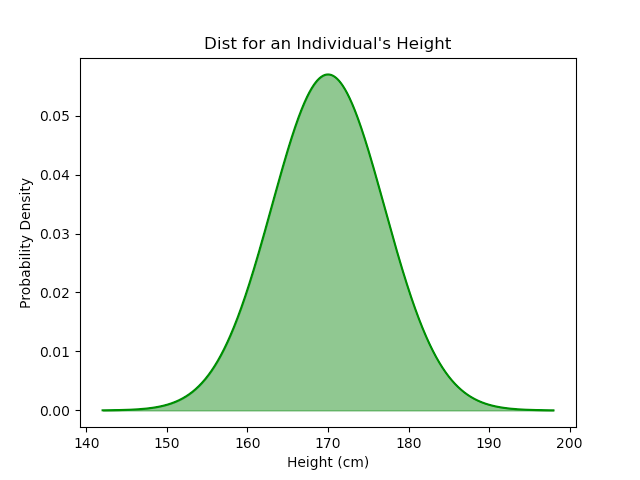
A very simple way we might generate a normal distribution for height is by assuming that everyone’s height comes from a shared, identical Gaussian distribution. This straightforwardly results in a normal distribution.
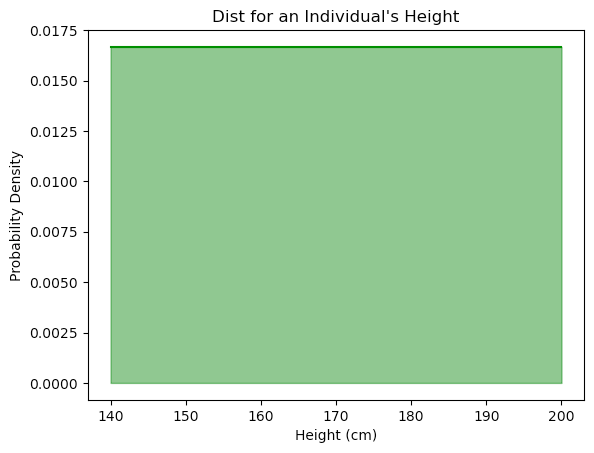
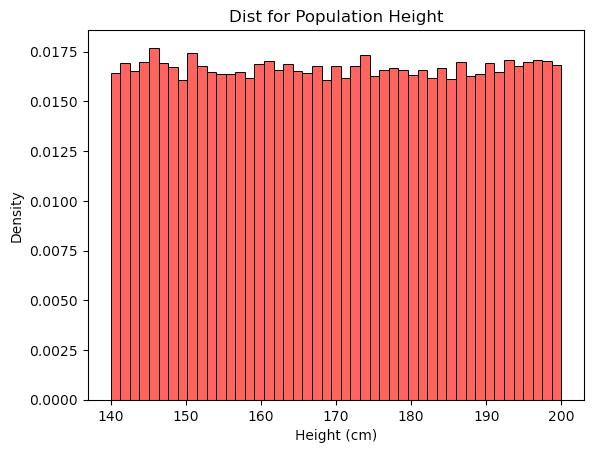
However, at this point, we have only accounted for the Gaussian distribution by assuming it earlier. The CLT has not yet been applied, so there is no clear justification for the appearance of the normal distribution. Indeed, the CLT provides no insight here since we are just doing Monty Carlo simulation and the height distribution will just match whatever we assume the shared, identical distribution to be. For example, a uniform distribution would result in a uniform distribution:
So how can we introduce the CLT?
Example 2: Sampling averages
A simple way to introduce the CLT is to make the distribution of every individual’s height a sum or average of many independent and identically distributed variables e.g. effects of many smaller impact genes. This allows us to better justify a normal distribution for each individual by applying the CLT and makes the population distribution normal (B1) as shown above. It also allows the model to say that differences in human height are strongly attributable to genetic factors (the small impact genes) (B2).3
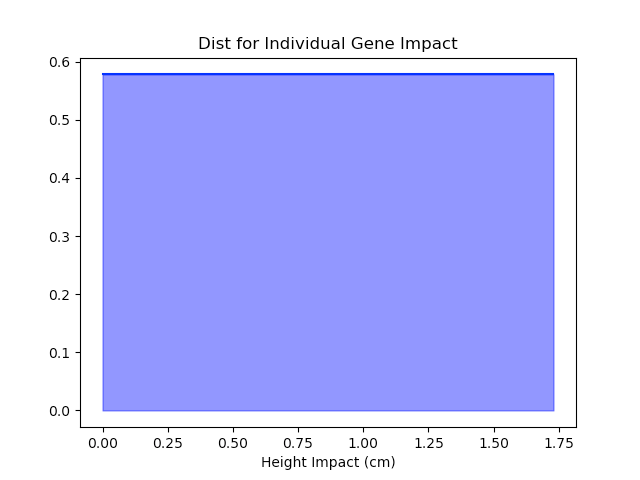
Unfortunately, though this construction can account for the population-level Gaussian height distribution (B1) and the attribution of height to genes (B2), it does not account for the heritability of height (B3). In order for height to be heritable, it must be the case that heights are not all drawn from an identical distribution, instead the children of taller parents are drawn from a taller distribution than the children of shorter ones. This is the source of my personal confusion.
The Central Limit Theorem can be applied at the individual level if you model an individual’s height as the sum of many independent, identically distributed effects (genes, environment). However, the distribution of population heights is not a sum or average, it is just the collection of heights for each individual. As we will see next, once we allow heights to be drawn from different distributions (even Gaussian ones), the CLT no longer applies and a normal distribution stops being guaranteed.
Example 3: Heritable heights
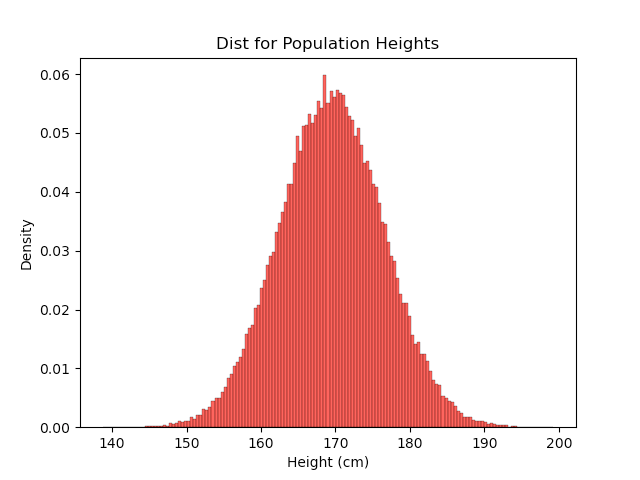
To understand the effects of heritability, let’s start with a simple model where an individual’s height is determined by the sum of independent, identically distributed variables as before, allowing the CLT to apply. However, we will also shift the centers of the distributions so that some are taller and some are shorter on average. The graph below shows the simulated population distribution for a case where the averages of individuals’ height distributions are evenly distributed from 150 cm to 220 cm.
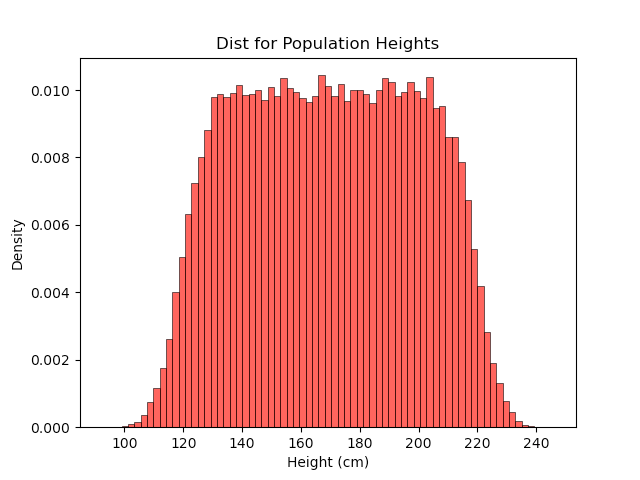
This population distribution looks similar to a normal distribution in the tails, but ultimately, it is clearly not the normal distribution. This shows that the fact heights are normally distributed at the individual level is not sufficient to achieve a normal distribution at the population level.
Still, is there anything more we can do to produce a normal distribution in the face of heritable traits? To see, let’s add a dynamic, generational element to our model.
Example 4: Generational change
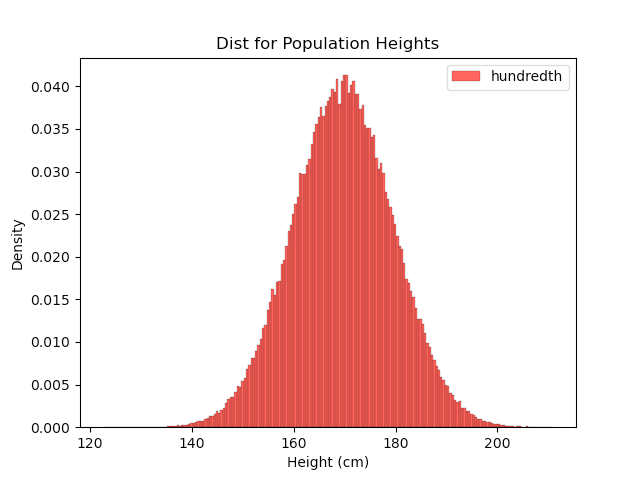
Our prior population was constructed in a vacuum, with the initial height distributions just taken as given. This time, let’s model the population over multiple generations to see how the distribution changes. To do this, we will assume a simple model where every person has a single, randomly chosen partner and two children. The children will then have their heights drawn from a Gaussian distribution centered at the average of their two parents’ heights. Simulating this with a starting distribution equivalent to the prior example, we get this outcome:
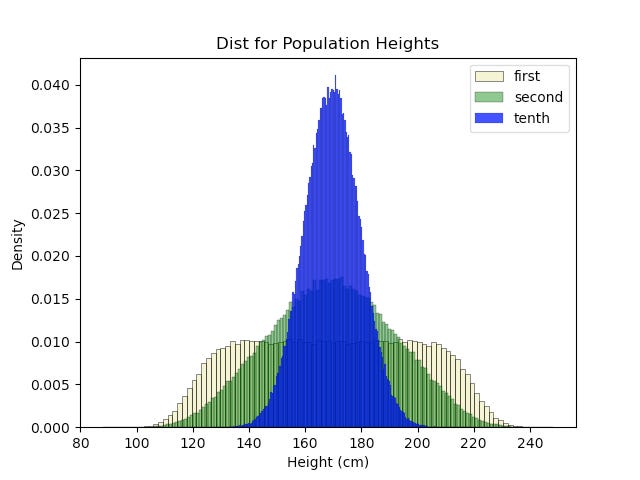
Looking at this, it seems that the distribution converges to the original normal distribution we had above.
So why is this happening? To be honest, I am not entirely sure. One point that I expect is relevant is that the distribution of the average of two independent Gaussians is also a Gaussian. This meant that the distribution of centers for the next generation’s heights was always a combination of Gaussians.
Final Thoughts
I decided to write this post because I was confused by casual references made to the Central Limit Theorem when height is discussed4 and how heritability clearly violated a condition for the CLT to apply directly to the population. I hope I have managed to demonstrate why that confusion was reasonable as well as highlight a possible resolution for why height is actually normally distributed.
Let me know if you have any other cases where using the normal distribution seems somewhat unjustified, if you have any good resources on mathematics for biological subjects, or if you know the real explanation for why height is normally distributed.
{Reminder: I am not an expert on this and my toy model is not meant to be accurate to the real world.}
{Code used to generate my diagrams is available at https://github.com/ohmurphy/height-and-clt.}
Fun fact: the ‘Central’ in Central Limit Theorem just refers to the theorem’s importance in probability theory, not anything about the theorem itself. It might as well be named the ‘Super Important Limit Theorem’ (SILT).
This Our World in Data page explicitly invokes the Central Limit Theorem when explaining that human height is normally distributed.
Allowing both genes and environment is fine as long as they can be combined as the sum of independent Gaussians. This works because a sum of independent Gaussians is also a Gaussian.
Again, see this Our World in Data page.


Actually only the strongest version of CLT demands identical distribution. The Lyapunov version only needs distributions with finite variance, and some extra conditions that most real world distributions would meet.
I think (I am no geneticist) that height would depend on a lot of different genes, each adding or subtracting a small amount. Like a person from x population will have y percent chance to have gene z which adds one milimeter to his height. Then on top of that you would have environmental effects.
Also with your example that multiple populations with different distributions of height might not add up to one normal distribution, I think that is exactly what you see in for example areas of Africa where Bantu people and Pygmy are living next to each other.
The conditions of the central limit theorem are sufficient to produce a normal distribution, but not necessary. (They are necessary for the central limit theorem to apply, but you are allowed to get normal distribution in other ways.)
Btw, height is obviously not normal distributed, because a normal distribution would assign non-zero probability to negative height.
So we'd need to discuss what kind of approximation to a normal distribution height could be?